How To Use Efficient Algorithms To Save Yourself From A Box-Catastrophe 

The Bin Packing Problem (BPP) is a classic optimization problem with applications in a wide range of industries, including commerce, logistics, transportation, manufacturing, and distribution. The objective of the BPP is to pack a set of items into a minimum number of bins, each of fixed capacity, such that the total weight or volume of the packed items does not exceed the capacity of any bin [1][2].

Imagine you have a truck to deliver all the pipes, valves, and fixtures to a construction site. The bin packing problem is how to fit all these items into the truck while minimizing wasted space and ensuring that the weight limit is not exceeded. It’s like Tetris in real life, but instead of colorful blocks, you’re packing items into bins.

Doing this efficiently takes a lot of Math. But is it even worth solving?

Why Is The Bin Packing Problem Important?

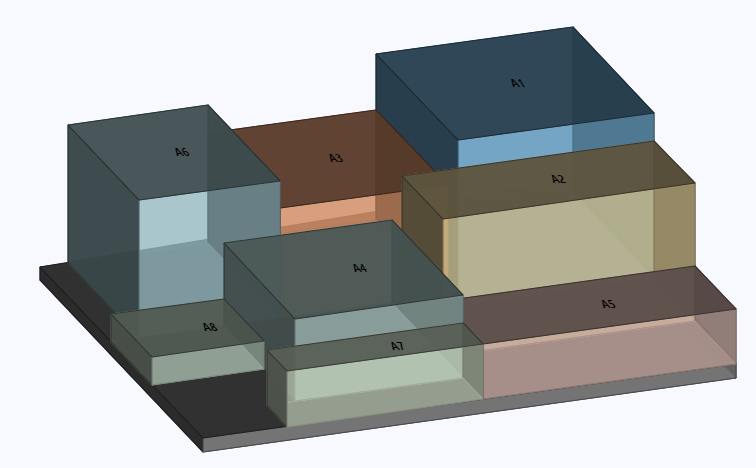
(Simulation of boxes placed in a shipping container. Image by the Author.)

An optimal bin packing strategy can save money, improve efficiency and reduce environmental impact in a variety of real-world applications, particularly B2B and B2C hard goods manufacturers and distributors.

(Opportunities to optimize bin packing in commerce manufacturing and distribution. Image by the Author.)

Efficient packing and shipping are critical to reducing transportation costs[3] and maximizing profit margins, which is especially important in the highly competitive e-commerce industry. By using BPP algorithms, these businesses can determine the optimal number of boxes required for each shipment of raw materials or bulk products. This allows an effective way to pack each pallet in the container or truck to minimize unused space and reduce the overall volume of the shipment. This reduces transportation costs and minimizes the environmental impact of shipping by reducing the number of trips required to procure the same number of products.

Moreover, the BPP can help eCommerce businesses streamline their warehouse operations by optimizing the use of storage space. Knowing how to utilize and optimize space to the fullest potential is critical to realizing an efficient and well-balanced warehouse[4]. By using BPP algorithms to pack products into storage bins, businesses can maximize the use of available space, reduce the time required to retrieve products, and minimize the need for additional warehouse space. This can result in significant cost savings, particularly for businesses that operate in densely populated urban areas where space is at a premium.

Furthermore, the BPP can be used to optimize order fulfillment operations in eCommerce businesses by packing multiple orders into a single box or calculating the optimal shipping box sizes. Businesses can reduce the number of shipments required and minimize the time and cost associated with picking and packing individual orders [5]. This can also lead to improved customer satisfaction by reducing the time required for product delivery.

How Do We Solve The Bin Packing Problem?

The Bin Packing Problem can be very difficult to solve. There is no known efficient algorithm to solve it exactly without trying every single possible way, which gets even more difficult with an increasing number of boxes. However, there are a number of heuristic techniques that can be used to find good solutions[7]. Some well-known simple solution methods are Shelf, Guillotine, and Maximal Rectangle Algorithms[1].

The Shelf Algorithm is a simple algorithm that works by dividing the available space into a sequence of shelves, each of which has a fixed height. The algorithm then packs the boxes into the shelves bottom-right-first to minimize the amount of wasted space.

(Packing using the Shelf Algorithm. Image by the Author.)

The technical implementation is very straightforward. There are a few choices you can make while placing the box.

• Place the box on the first shelf that fits it
• Place the box on the shelf that does not increase the height, creating a new shelf if required.
• Place the box on the shelf that produces the least space left after the placement.

The choice depends on the use case. For example, only the first choice above applies when packing a container that is closed off on three sides and open only on the top.

The Guillotine Algorithm starts by placing a box in the corner of the best available space, after which the L-shaped free space is split into 2 disjoint free spaces. While it is computationally more intense than the shelf algorithm, it reduces space wastage.

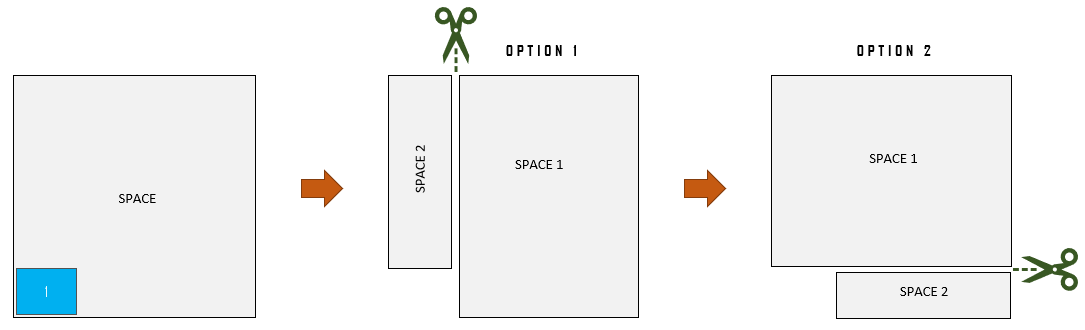
(Guillotine cut: splitting the space after box placement. Image by the author.)

After the placement of the first box bottom-right in the image above, the algorithm splits the remaining space into 2 rectangles. The choice of which way to split can be made on maximum length or similar areas, or avoiding small spaces. We pick the best-fit space for the second box and repeat the split. This continues until we can no longer place a box in the bin.

(Filling the space with Guillotine Algorithm. Image by the Author.)

Like the shelf algorithm, there are some implementation choices you can make:

• Pick the space with the best area fit. Try all spaces and see which one has the least remaining space after placement.
• Pick the space that fits the best in terms of width or height.

In one of our implementations, we used the best width, and if the widths were the same, also used the best height.

The Maximal Rectangle Algorithm is an improvement over the Guillotine Split Algorithm in that we create two overlapping rectangular spaces inside an L-shaped space. It performs better in terms of its ability to use space more efficiently, but is more computationally intensive.

So, instead of choosing option 1 or option 2 in the Guillotine Algorithm, we choose both.

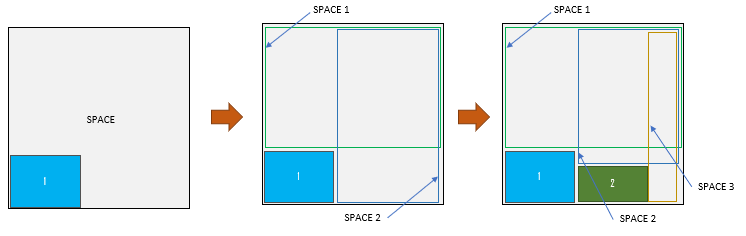
The space in the second square above shows the green and blue spaces 1 and 2 that the system tracks. When a new box needs to be placed, we evaluate the two spaces and pick one. Placing the new box 2 in space 2 does not impact space 1 in this case. So, we split space 2 into spaces 2′ and 3.

Now, let’s look at a more complicated case.

(Placement of boxes. A more complicated case. Image by the Author.)

In the square numbered 2 in the above picture, the placement of box A2 impacts the free spaces F1 and F2. We split F1 into F3 and F4 and F5 (the small red box at the bottom. Meanwhile, F2 is split into F6 (the red box at the bottom left) and F7. The next phase of the algorithm deduces that F5 is contained within F7 and F6 is contained within F3. These are hence removed. We end up with 3 free spaces F3, F4, and F7 as shown below.

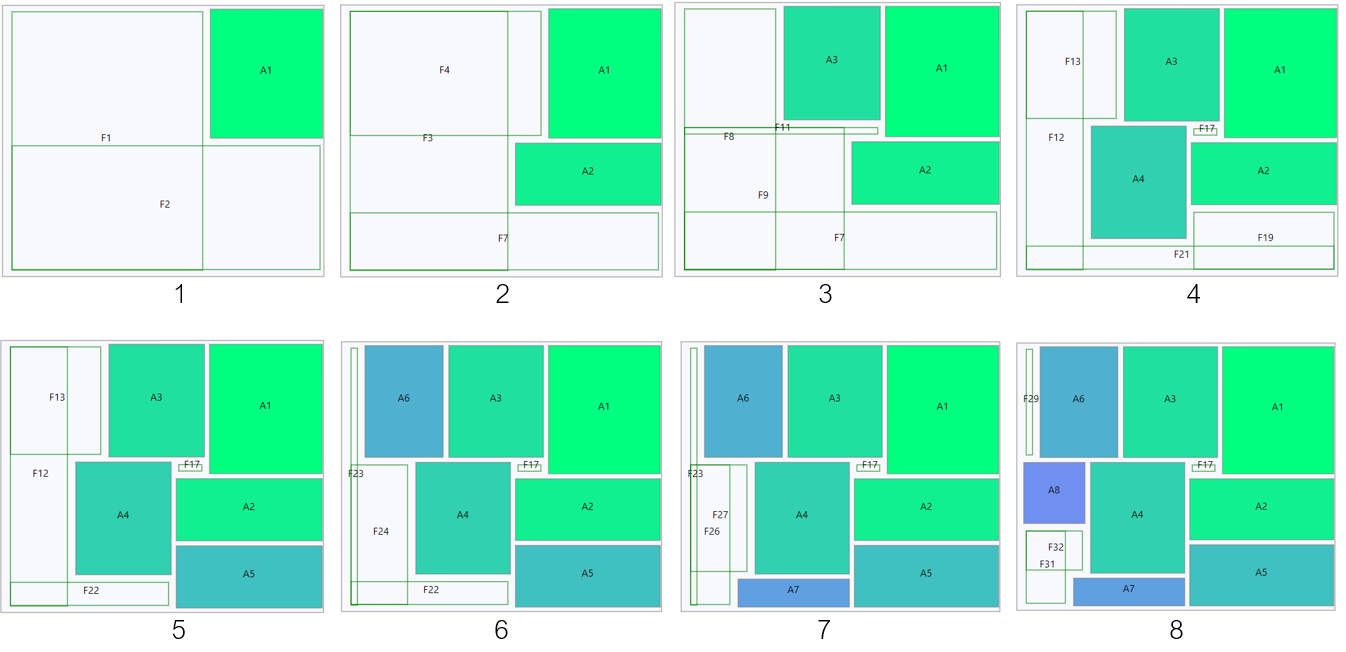
(Free rectangles as boxes are placed. Image by the Author.)

The placement of boxes then continues consuming, splitting, merging, and removing free spaces, as shown above. As with the other algorithms discussed above, we have some implementation choices: Place the box in a space that leaves the least amount of free space. Place the box in a space that leaves the least width or height, or both. In the picture shown above, we used an algorithm that picks a free space with perfect length or width matching, and if none are found, pick a free space with the least area wastage. The choice you make will depend on your use case. The algorithms discussed so far are simple to implement and can be used to find good solutions to the bin-packing problem. However, they are not always optimal and, in some cases, will use more bins than the best solution. They are a good choice for concerns where speed is more important than space optimization. These algorithms can then be combined with other optimization techniques, such as Genetic Algorithms, Simulated Annealing, etc. Genetic Algorithms, for example, can start with the result of any of the algorithms above as an initial population and iterate with selection, combination, and mutation, picking the best of the offspring solutions until it produces results that waste less space. In some cases, where speed is not critical and the number of boxes is small, such as in shipping container packing, Dynamic Programming or a Brute-force Algorithm can be implemented to find the absolute best fit similar to that of the Knapsack Problem [8]. Brute-force algorithms, for example, will place each of the boxes in every possible sequence, dutifully noting down the space wastage and print out a result of the least space-wasting arrangement at the end of the run.

Now that we have covered Math, how can we leverage it to our advantage in e-Commerce? At work, I have dealt with the Bin Packing Problem in various situations. Some examples are consignment goods storage, custom truck and rail car packing, and customer shipments. While there are commercial tools available to solve the bin packing problem, some cases warrant implementing a customized and tweaked algorithm.

For consignment goods storage at client warehouse locations, we use a customized Guillotine Algorithm. The algorithm attempts to stack similar items on top of each other to facilitate easy access. Consignment inventory can add breadth and depth to the manufacturer’s market opportunity and increase sales and profits [9].

For custom truck packing, shoppers use a visualization tool to add items to a truck and see it filling up. It displays results in real-time, so online shoppers can be confident that they will receive the goods they ordered and that they are fully leveraging the truck that they paid for. The algorithm is designed to be implemented in an ORO Commerce Cloud environment and produces quick graphical results for the shoppers.

A rail car packer application uses a generic version of a Maximal Rectangle Algorithm with special restrictions on proximity placement as chemicals are being transported. In addition, we use a genetic algorithm to optimize the placement further by starting with the above results as an initial population and then iterating over it until better results with less space wastage are found.

A customer shipment packer application uses a fast version of the Shelf Algorithm, which tells the order-picking staff how best to place the items in the shipping box without knowing any other boxes coming down the belt bound to the same location. We use a slight optimization to recommend placing the item on a bottom shelf if the algorithm detects that the space is accessible.

Finally, we use a full Brute-force implementation for Ship container optimization, as the contents of the container and their dimensions are known well in advance. Since most of the items on the container are pallets, we can run the simulation offline and store the most optimal solution to be used by the loading crew. While this might seem like an overkill, it’s really worth the effort, considering the cost of container shipping and readily available power from cheap cloud computing units.

Comprehending these algorithms in depth helps with understanding the cost vs. benefit of picking one algorithm over the other. It is surprising how many developers will simply pick a ready-made app or library to perform this task without understanding the implications when there are millions of dollars at stake.

The BPP is a critical tool for e-commerce businesses looking to optimize their operations and reduce costs. By using BPP algorithms, businesses can efficiently pack and ship products, optimize warehouse space utilization, and streamline order fulfillment operations. This, in turn, can help businesses remain competitive in the highly competitive e-commerce industry and provide better value to their customers, with the additional benefit of reducing the impact they have on the environment.

If you would like to learn more about how to utilize BPP algorithms or examine how efficiently your organization is currently tackling the Bin-Packing problem, get in touch with our eCommerce and technology experts at AAXIS Digital.    

Book A Consultation

References

[1] Jylanki, Jukka (2015), “A Thousand Ways to Pack the Bin — A Practical Approach to Two-Dimensional Rectangle Bin Packing”, http://pds25.egloos.com/pds/201504/21/98/RectangleBinPack.pdf

[2] Various Authors (2023), “Bin packing problem”, Wikipedia, https://en.wikipedia.org/wiki/Bin_packing_problem

[3] Russell, Dawn; Coyle, John J.; Ruamsook, Kusumal; Thomchick, Evelyn A. (2014) “The real impact of high transportation costs”, CSCMP’s Supply Chain Quarterly, https://www.supplychainquarterly.com/articles/838-the-real-impact-of-high-transportation-costs

[4] Engeler, James R. (2021), “Space Optimization in warehouses”, University of Wisconsin, Seminar Paper. https://minds.wisconsin.edu/bitstream/handle/1793/82578/Engeler.%20James.pdf?sequence=1&isAllowed=y

[5] Optioryx (2023), “Choosing The Shipping Box Dimensions That Fit Your Order Profile”, Medium, https://medium.com/@optioryx/choosing-the-shipping-box-dimensions-that-fit-your-order-profile-729a3ea01de7

[6] Moussa, Ahmad (2021), “Rectangle Packing: An Incredibly Difficult Problem”, Gorilla Sun, https://gorillasun.de/blog/rectangle-packing-an-incredibly-difficult-problem

[7] Martello, Silvano; Toth, Paolo (1990), “Bin-packing problem — Knapsack Problems: Algorithms and Computer Implementations”, Chichester, UK: John Wiley and Sons, http://www.or.deis.unibo.it/kp/Chapter8.pdf

[8] Sharma, Prashant (2022), “Knapsack Problem in Python”, Analytics Vidhya, https://www.analyticsvidhya.com/blog/2022/05/knapsack-problem-in-python/

[9] Nicasio, Francesca (2022), “What is Consignment Inventory and How Does It Work?”, Vendhq Blog, https://www.vendhq.com/blog/consignment-inventory/